Chimera-like states in modular networks

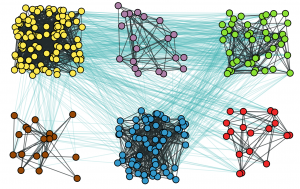
Inspired by the ancient Greek mythological creature Chimera (χίμαιρα) which had a lion’s head, a goat’s body and a serpent’s tail, Abrams and Strogatz [1] coined the term “chimera states” for the counterintuitive self-organized phenomenon in which synchronous and desynchronous oscillatory behavior coexist in the same system, first found by Kuramoto and Battogtokh [2]. It is believed that these states may be related to unihemispheric sleep, observed in birds and dolphins, as they are found to sleep with one eye open, meaning that half of their brain is synchronized whilst the other half is desynchronized.

Chimera states were previously analyzed in complex networks. However, they have not been extensively studied in modular networks, where interactions within and across modules are attributed to different types of links that play their own roles in the self-organized dynamics. Here, we consider the neural network of the C.elegans soil worm, equipped with electrical and chemical neural synapses for communication. Using a community detection method, we split its neural network into six interconnected communities as shown below:

We also assume that neurons obey chaotic bursting dynamics given by the Hindmarsh-Rose system and are connected with electrical synapses (dark gray links) within their communities and with chemical (cyan links) across them. The described network-organized system has the form,

[
\dot{p}i = q_i-a p_i^3+bp_i^2-n_i+I{\text{ext}}+\color{#222A2B}{g_{el}\sum_{j=1}^{N}L_{ij}H(p_j)}-\color{#45B6B6}{g_{ch}(p_i-V_{\text{syn}})\sum_{j=1}^{N}T_{ij}S(p_j)},\[2pt]
\dot{q}_i = c-dp_i^2-q_i,\[2pt]
\dot{n}_i = r[s(p_i-p_0)-n_i],
]

where (i=1,\ldots,N) is the neuron index, (p_i) is the membrane potential of the (i)-th neuron, (q_i) is associated with the fast current and (n_i) with the slow current. The parameters are chosen such that the system exhibits a multi-scale chaotic behavior characterized as spike bursting. (r) modulates the slow dynamics of the system so that each neuron lies in the chaotic regime (see [3] for details).

The connectivity structure of the electrical synapses is described in terms of the Laplacian matrix (\mathbf{L}). The strength of the electrical coupling is given by the parameter (g_{el}) and its functionality is governed by the linear function (H(p)=p).

The connectivity structure of the chemical synapses is described in terms of the adjacency matrix (\mathbf{T}). The chemical coupling is nonlinear and its functionality is described by the sigmoidal function (S(p)={1+\exp[-\lambda(p-\theta_{\text{syn}})]}^{-1}\,), which acts as a continuous mechanism for the activation and deactivation of the chemical synapses. The coupling strength associated to this type of synapses is (g_{ch}).

The coaction of these synapses with the dynamics was studied in [3] and revealed that they were able to drive the dynamics to the emergence of chimera-like states, evidenced by the coexistence of strongly synchronized and desynchronized communities of neurons. A topological analysis of the network’s structure has revealed that the most populated communities drive this peculiar phenomenon, being the most influential among all (see [3] for more details).

Synchronous oscillations:

Desynchronous oscillations:

Chimera-like state:

Further reading:

1. Y. Kuramoto and D. Battogtokh:
   Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators.
   NONLINEAR PHENOMENA IN COMPLEX SYSTEMS5(4) 380-385 (2002).
   [journal]
2. D. M. Abrams and S. H. Strogatz:
   Chimera States for Coupled Oscillators.
   Phys. Rev. Lett.93 174102 (2004).
   [PRL]
3. J. Hizanidis, N. E. Kouvaris, G. Zamora-Lopez, A. Diaz-Guilera and C. Antonopoulos
   Chimera-like states in modular neural networks.
   Scientific Reports 6, 19845 (2016).
   [Scientific Reports][arXiv]