Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions
|
Experiments with networks of discrete reactive bistable electrochemical elements organized in regular and nonregular tree networks are presented to confirm an alternative to the Turing mechanism for the formation of self-organized stationary patterns. The results show that the pattern formation can be described by the identification of domains that can be activated individually or in combinations. The method also enabled the localization of chemical reactions to network substructures and the identification of critical sites whose activation results in complete activation of the system. Although the experiments were performed with a specific nickel electrodissolution system, they reproduced all the salient dynamic behavior of a general network model with a single nonlinearity parameter. Thus, the considered pattern-formation mechanism is very robust, and similar behavior can be expected in other natural or engineered networked systems that exhibit, at least locally, a treelike structure. One-component bistable systems organized on undirected networks, generally reads where $u$ is the local activator density, function $f(u_i,h)=u_i(h-u_i)(u_i-a)$ specifies local bistable dynamics and $D$ is the coupling strength. $\mathbf{T}$ is a symmetric ($T_{ij} = T_{ji}$) adjacency matrix that describes the connectivity structure of the network; its elements are $T_{ij}=1$, if there is a link connecting the nodes $i$ and $j$ $(i,j=1,…,N$), and $T_{ij}=0$ otherwise.
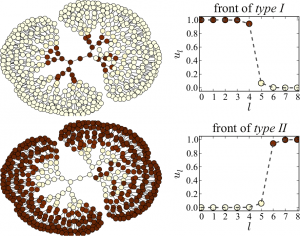
Bistable treesIn the figure below we see a regular tree with the branching factor $r$. In such a tree, all nodes, lying at the same distance $l$ from the origin, can be grouped into a single shell (see figure above). The tree can then be treated as a chain of $l = 1,2,3,\ldots$ asymmetrically coupled shells. Suppose that we have taken a node which belongs to the shell $l$. This node should be diffusively coupled to $r$ nodes in the next shell $l+1$ and to just one node in the previous shell $l-1$. Introducing the activation level $u_l$ in the shell $l$, the evolution of the activator can therefore be described by the equation This latter equation can be analysed (see [1,2]) and reveal the dynamical behaviour that is summarized in the next bifurcation diagram.
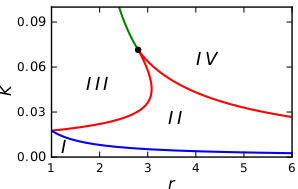
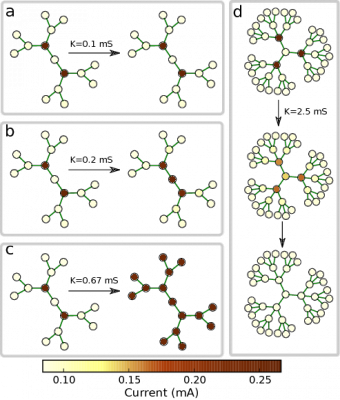
The bifurcation diagram in $r-K$ parameter space describes the dynamical behaviour of an activation in regular trees of coupled bistable chemical reactions, with coupling strength $K$ and branching ratio $r$: Region I: The activation is pinned. Experiments with regular tree networks of coupled bistable electrochemical reactionsThis dynamical behavior has also been verified in experiments with networks of coupled bistable electrochemical reactions. Each node of that network represented corroding metal (nickel) wire that accommodated a complex reaction system that exhibits bistable behavior. The active state corresponds to a high current, and the passive state to a low current. Moreover, coupling is established in the form of a charge flow between the wires, which affects the rate of metal dissolution of the coupled electrodes. Electrodes and external connections between them correspond to the nodes and the links of the networks.
The above figure shows the evolution observed in the same network after the activation of intermediate nodes at different coupling strengths. In region I (panel a), the fronts are pinned on both sides. In region II (panel b), the center-facing front spreads towards the center, and the periphery-facing front is pinned. In region III, fronts spread in both directions and finally activate the entire network (panel c). In region IV, the center-facing front propagates towards the center, but the periphery-facing front retreats from the periphery finally establishing a passive state in the entire network (panel d). All these experiments confirm the theoretical predictions for regular tree networks. Experiments with nonregular tree networks of coupled bistable electrochemical reactionsThe following movie shows an example from the experiments where bistable electrochemical reactions are coupled in a non-regular tree network. We see that a stationary pattern is finally formed as the initial activation gets pinned on some nodes with critical branching ratio.
Further reading:
|