Stationary patterns in star networks of bistable units: Theory and application to chemical reactions

By nkoub / April 2, 2017 / Bistable systems, experiments, Networks, pattern formation, stationary patterns / No Comments

We present theoretical and experimental studies on pattern formation with bistable dynamical units coupled in a star network configuration. By applying a localized perturbation to the central or the peripheral elements, we demonstrate the subsequent spreading, pinning, or retraction of the activations; such analysis enables the characterization of the formation of stationary patterns of localized activity. The results are interpreted with a theoretical analysis of a simplified bistable reaction-diffusion model. Weak coupling results in trivial pinned states where the activation cannot propagate. At strong coupling, uniform state is expected with active or inactive elements at small or large degree networks respectively. Nontrivial stationary spatial pattern, corresponding to an activation pinning, is predicted to occur at intermediate number of peripheral elements and at intermediate coupling strengths, where the central activation of the network is pinned, but the peripheral activation propagates toward the center. The results are confirmed in experiments with star networks of bistable electrochemical reactions. The experiments confirm the existence of the stationary spatial patterns and the dependence of coupling strength on the number of peripheral elements for transitions between pinned and retreating or spreading fronts in forced network configurations (where the central or periphery elements are forced to maintain their states).

An illustrative bistable systems organized on undirected networks, generally reads $\dot{u}_i = u_i(h-u_i)(u_i-a) + K \sum_{j=1}^{N}\!T_{ij}\left(u_j - u_i \right)$

where $u$ is the local activator density, function $f(u_i,h)=$ specifies local bistable dynamics and $D$ is the coupling strength. $\mathbf{T}$ is a symmetric ($T_{ij} = T_{ji}$) adjacency matrix that describes the connectivity structure of the network; its elements are $T_{ij}=1$, if there is a link connecting the nodes $i$ and $j$ $(i,j=1,…,N$), and $T_{ij}=0$ otherwise.

In the star networks, because of the symmetry in the system all peripheral nodes obey the same equation and the system is reduced into a two-dimensional system of ordinary differential equations,

$\dot{u} = u(h-u)(u-a) + kK(v-u) := f(u,v;k,K)\,,$ for the central hub
$\dot{v} = v(h-v)(v-a) + K(u-v) := g(u,v;K)\,,$ for the peripheral nodes

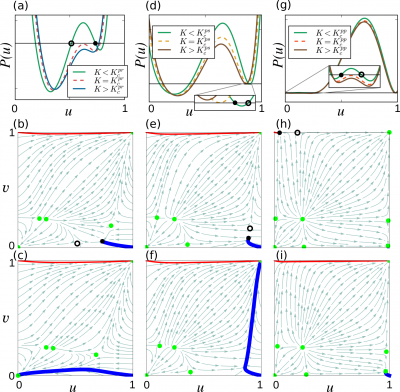
By solving $f(u,v;k,K)=0$ we can get an expression of $v$ in terms of $u$, and then, by substituting this expression into the equation $g(u,v;K)=0$, we obtain the sixth degree polynomial equation,

$P(u) := c_0 + c_1 u + c_2 u^2 + c_3 u^3 + c_4 u^4 + c_5 u^5 + u^6 = 0\,,$

The following figure shows $P(u)$ for $k=10$ and three values of coupling strength $K$. At $K_c^{pr}$ (dashed curve) the two inner roots (shown with circle and dot) of $P(u)$ merge together and disappear through a saddle-node bifurcation. These roots correspond to the fixed points of the system. Any initial condition $(u_0,v_0)$ in the basin of attraction of a stable fixed point will eventually converge to the corresponding fixed point. Therefore, before the bifurcation, the initial center activation $(a,0)$ results in a stationary pattern (thick blue trajectory in panel (b)), and the initial periphery activation $(0,a)$ propagates towards the center (thin red trajectory in panel (b)). After the bifurcation, the center activation retreats to the passive state (thick blue trajectory in panel (c)) whereas the periphery activation propagates towards the center (thin red trajectory in panel (c)). Figures (d)–(f) and (g)–(i) illustrate similar scenarios for $k=5$ and $k=3$ respectively.

Further reading:

Stationary patterns in star networks of bistable units: Theory and application to chemical reactions. N. E. Kouvaris, M. Sebek, A. Iribarne, A. Diaz-Guilera and I. Z. Kiss, Phys. Rev. E 95, 042203 (2017). [arXiv]
Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions. N. E. Kouvaris, M. Sebek, A. S. Mikhailov and I. Z. Kiss
Angew. Chem. 2016, 128, 13461-13464.
[Angew. Chem.]
Angew. Chem. Int. Ed. 2016, 55, 13267-13270.
[Angew. Chem. Int. ed.]
[arXiv]