Excitable networks

Excitation waves are studied on trees and random networks of coupled active elements. Undamped propagation of such waves is observed in those networks. It represents an excursion from the resting state and a relaxation back to it for each node. However, the degrees of the nodes influence drastically the dynamics. Excitation propagates more slowly through nodes with larger degrees and beyond some critical degree waves lose their stability and disappear. For regular trees with a fixed branching ratio, the critical degree is determined with an approximate analytical theory which also holds locally for the early stage of excitation spreading in random networks.

Let us assume a complex network of coupled excitable neurons governed by the FitzHugh-Nagumo dynamics,

\[\dot{u}_i = f(u_i,v_i) + D\sum_{j=1}^{N}\! L_{ij}u_j
\\[2pt]
\dot{v}_i = \varepsilon g(u_i,v_i) \]
where \(f(u,v)=u-u^{3}/3-v\) and \(g(u,v)=u-\beta\). \(u_i\) and \(v_i\) are the densities of activator and inhibitor species in node \(i\). The summation term with the Laplacian matrix \(L\) describes diffusive coupling, and the constant \(D\) is the corresponding coupling rate. \(\varepsilon\) represents the ratio of their characteristic time scale.

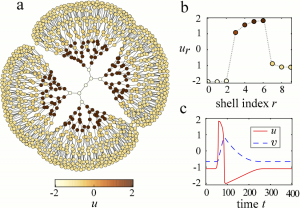
This figure shows a snapshot of an excitation wave which propagates from the root towards the periphery in a regular tree of 10 shells with branching ratio (a). The wave can also be represented as a pulse by grouping the nodes with the same distance from the root into a single shell (b). The time evolution of a single node (or shell) is shown in (c).

In our approximation, instead of investigating propagation of excitation waves directly on a tree network (a) we study it, using the sequence of coupled shells (b) described by equations:

\[\dot{u}_r = f(u_r,v_r) + D [u_{r-1}-ku_{r} +(k-1)u_{r+1}]
\\[2pt]
\dot{v}_r = \varepsilon g(u_r,v_r) \]

Contrary to chains \(k=2\), where both propagation directions (left or right) of excitation waves are equivalent, propagation from the root to the periphery of a tree \(k>2\) is physically different from the propagation in the opposite direction, i.e. towards the tree root. Here, only excitation waves that start from the root which can — under appropriate conditions — propagate towards the periphery are considered.

Excitation waves can be generated by applying a large enough external perturbation to the root of the tree while all other nodes are in the resting state. This perturbation can excite the root. Subsequently, it is possible for excitation to be passed from one node to another, due to the diffusional transport of the activator and it reaches nodes within the same shell at the same time. Thus, propagation of undamped excitation waves, which represent an excursion from the resting state and a relaxation back to it for each node of the tree, can be supported (see figure above).

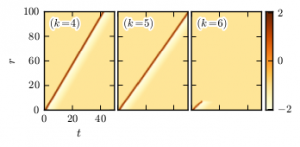
Not all excitable trees can, however, lead to such propagating waves.

In the figure above we see for a given set of parameters that excitation waves can propagate from the root towards the periphery in trees with \(k=4\) and \(k=5\). However, trees with larger branching ratio, e.g. \(k=6\), fail to support the undamped propagation of waves; starting from the root, excitation may be passed to all nodes of some shells with short distance (shortest path length) from the root, but then fails to propagate further and vanishes (see spacetime plots for \(k=6\)).

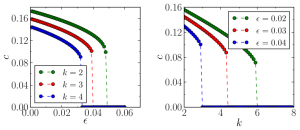
Numerical simulations have revealed that excitation waves propagate more slowly in trees with larger \(k\). As \(k\) increases, it reaches a critical value where waves propagate with the minimum (positive) velocity. In contrast to bistable trees, where fronts can be pinned or retreated as \(k\) becomes larger, excitation waves cannot stop or reverse the direction of their propagation. They become unstable and disappear beyond this critical degree. When \(k\) is fixed, the same transition to unstable waves occurs when some critical value of the time scale separation constant \(\varepsilon\) is exceeded (see next figure).

The stability analysis of these waves is performed with a numerical continuation method; we have also introduced a kinematical theory (see details in [1]). Both methods, numerical and analytical, reveal that the destabilisation of the waves takes place through a saddle-node bifurcation which occurs at the critical degree (or \(\varepsilon\)). Next movie illustrates an unstable excitation wave:

Application to random networks

Propagation failure of excitation waves has also been observed in random networks. Here we provide an example of system on an Erdös-Rényi network, where the hub node is initially set in the excited state. Consequently, excitation propagates to certain neighbouring nodes and finally disappears. This behaviour can be understood by our approximate theory for the trees, which holds also locally, for the early stage of propagation, in random networks. An interesting behaviour that appears in random networks is that excitation may follow certain paths and not others, depending on the degrees of the corresponding nodes (numbers in the nodes represent their degrees).

Further reading:

1. N. E. Kouvaris, T. M. Isele, A. S. Mikhailov and E. Schöll:
   Propagation failure of excitation waves on trees and random networks.
   EPL (Europhysics Letters) 106, 68001 (2014).
   [EPL] [arXiv]