Bistable tree networks: Traveling and pinned fronts
|
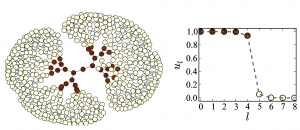
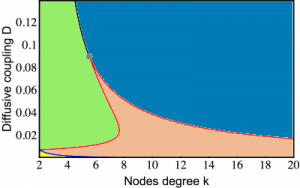
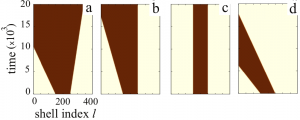
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable one-component systems on hierarchical tree networks. As revealed through numerical simulations, traveling fronts exist in network-organized systems. They represent waves of transition from one stable state into another, spreading over the entire network. The fronts can furthermore be pinned, thus forming stationary structures. While pinning of fronts has previously been considered for chains of diffusive coupled bistable elements, the network architecture brings about significant differences. An important role is played by the degree of a node. For regular trees with a fixed branching factor, the pinning conditions are analytically determined. Classical one-component reaction-diffusion systems in continuous media are described by the form where $u$ is the local activator density, function $f(u,h)=u(h-u)(u-a)$ specifies local bistable dynamics and $D$ is the diffusion coefficient. Depending on the particular context, the activator variable $u$ may represent concentration of a chemical reagent or of biological species which amplifies its own production. Here we consider analogues of this bistable system, which are taking place on networks. In network-organized systems, the activator species occupies nodes of a network and can be transported over network links to other nodes. The connectivity structure of the network can be described in terms of an adjacency matrix $\mathbf{T}$, whose elements are $T_{ij}=1$, if there is a link connecting the nodes $i$ and $j$ ($i,j=1,…,N$), and $T_{ij}=0$ otherwise. Processes in undirected networks, where the adjacency matrix $\mathbf{T}$ is symmetric ($T_{ij} = T_{ji}$), generally, are given by In the figure below we see a regular tree with the branching factor $k-1$, where $k$ is the nodes degree. In such a tree, all nodes, lying at the same distance $l$ from the origin, can be grouped into a single shell (see figure above). The tree can then be treated as a chain of $l = 1,2,3,\ldots$ asymmetrically coupled shells. Suppose that we have taken a node which belongs to the shell $l$. This node should be diffusively coupled to $k-1$ nodes in the next shell $l+1$ and to just one node in the previous shell $l-1$. Introducing the activation level $u_l$ in the shell $l$, the evolution of the activator can therefore be described by the equation This latter equation can be analysed (see [1]) and reveal all the dynamics of the bistable trees which support propagation, stationary and retreated fronts. The above bifurcation diagram in $k-D$ parameter space describes the dynamical behaviour of an activation in the bistable trees: a. Green region: The activation propagates towards the root and the periphery. We see this behaviour in the space-time plots below Based on the theory for the regular trees we can predict the behaviour of an activation set on a node or on a group of nodes in a non-regular tree. The video below shows that the activation can propagate through some nodes but gets pinned in front of other nodes, a behaviour that depends on the degree of those nodes. Further reading:
|