Pattern formation in multiplex networks

We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates heterogeneous patterns with significant differences from those observed in single-layer networks. Remarkably, diffusion-induced instability can occur even if the two species have the same mobility rates; condition which can never destabilize single-layer networks. The instability condition is revealed using perturbation theory and expressed by a combination of degrees in the different layers. Our theory demonstrates that the existence of such topology-driven instabilities is generic in multiplex networks, providing a new mechanism of pattern formation.

Activator-nhibitor system organized in a multiplex network

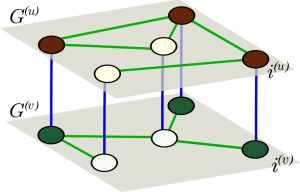We consider multiplex networks of activator and inhibitor populations, where the different species occupy separate network nodes in distinct layers. Species react across layers according to the mechanism defined by the activator-inhibitor dynamics, and diffuse to other nodes in their own layer through connecting links (see figure). Such a process can be described by the equations

[\dot{u}i(t) = f(u_i,v_i) + \sigma^{(u)}\sum{j=1}^{N}! L_{ij}^{(u)}u_j
\[2pt]
\dot{v}i(t) = g(u_i,v_i) + \sigma^{(v)}\sum{j=1}^{N}! L_{ij}^{(v)}v_j]
where (u_i) and (v_i) are the densities of activator and inhibitor species in nodes (i^{(u)}) and (i^{(v)}) of layers (G^{(u)}) and (G^{(v)}), respectively. The superscripts ((u)) and ((v)) refer to activator and inhibitor. The activator nodes are labeled by indices (i=1,2,\ldots,N) in order of decreasing degrees. The same index ordering is applied to the inhibitor layer. The functions (f(u_i,v_i)) and (g(u_i,v_i)) specify the activator-inhibitor dynamics. The summation terms with the Laplacian matrices (L^{(u)}) and (L^{(v)}) describe diffusion processes in the two layers, and the constants (\sigma^{(u)}) and (\sigma^{(v)}) are the corresponding mobility rates.

The onset of the instability occurs when (\text{Re}\,\lambda=0) for some pair of nodes (i^{(u)}) and (i^{(v)}). The instability condition is fulfilled when these nodes possess a combination of degrees (k^{(u)}) and (k^{(v)}) such that, the inequality
[ k^{(u)} \leq \frac{f_u g_v – f_v g_u – f_u \sigma^{(v)} k^{(v)} } {g_v \sigma^{(u)} – \sigma^{(u)} \sigma^{(v)} k^{(v)}}]

is satisfied. Here, \(f_u,f_v,g_u, g_v\) are partial derivatives at the uniform steady state.

Last equation (as equality) denotes a transcritical bifurcation where the Turing instability occurs and shows in the \( k^{(u)} -k^{(v)}\) plane with the red curve. In the same plane blue curve stands for a saddle-node bifurcation [1] and points denote the degrees of pair of nodes of a given multiplex network. 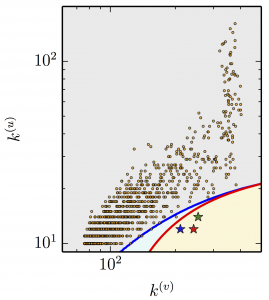The unstable nodes, where Turing instability occurs and the non-uniform pattern starts to develop, are denoted by stars. As it is seen in the following video, these nodes leave first the uniform steady state and then other nodes differentiate giving the final shape of the pattern, as shown in the movie below:

If many pairs of nodes have degrees in the unstable regime as defined by the instability condition above, then the non-uniform pattern that develops contains more nodes which differentiate from the uniform steady state. See an example in the following movie:

Further reading:

1. Pattern formation in multiplex networks.
   N. E. Kouvaris, S. Hata and A. Diaz-Guilera.
   Scientific Reports 5, 10840 (2015). [Journal]
2. Turing patterns in network-organized activator–inhibitor systems.
   H. Nakao and A. S. Mikhailov.
   Nature Physics 6, 544–550 (2010). [Journal]
3. The Turing bifurcation in network systems: Collective patterns and single differentiated nodes.
   M. Wolfrum.
   Physica D: Nonlinear Phenomena 241 (16), 1351–1357 (2012). [Journal]