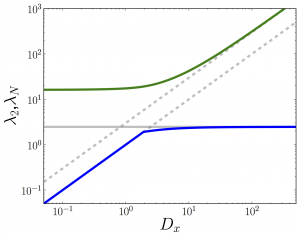
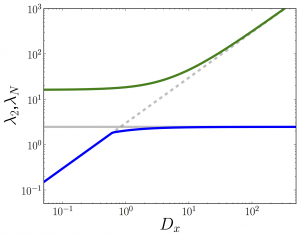
Multiplex networks: spectral properties
|
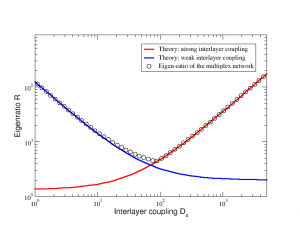
One of the more challenging tasks in the understanding of dynamical properties of models on top of complex networks is to capture the precise role of multiplex topologies. In a recent paper, Gómez et al. [Phys. Rev. Lett. 110, 028701 (2013)], some of the authors proposed a framework for the study of diffusion processes in such networks. Here, we extend the previous framework to deal with general configurations in several layers of networks and analyze the behavior of the spectrum of the Laplacian of the full multiplex. We derive an interesting decoupling of the problem that allow us to unravel the role played by the interconnections of the multiplex in the dynamical processes on top of them. Capitalizing on this decoupling we perform an asymptotic analysis that allow us to derive analytical expressions for the full spectrum of eigenvalues. This spectrum is used to gain insight into physical phenomena on top of multiplex, specifically, diffusion processes and synchronizability. Multiplex network with three layers connected as 1-2-3The smaller non-zero \(\lambda_2\) (blue) and the larger \(\lambda_N\) (green) eigenvalues are shown as a function of the interlayer coupling \(D_x\) with the theoretical lines (grey). Multiplex network with three layers connected as 1-2-3-1The smaller non-zero \(\lambda_2\) (blue) and the larger \(\lambda_N\) (green) eigenvalues are shown as a function of the interlayer coupling \(D_x\) with the theoretical lines (grey). Eigenratio of a multiplex network with two layerThe eigenratio \(R\)=\(\lambda_N\)/\(\lambda_2\) is shown as a function of the interlayer coupling \(D_x\) (circles) with the theoretical predictions for weak (blue) and strong (red) interlayer coupling. Details for the multiplex networks as well as the analytical calculations related to the analysis of spectral properties of their Laplacian matrix (so-called supra-Laplacian) can be found in the references cited below.
|