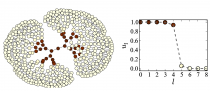
Bistable tree networks: Traveling and pinned fronts

Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable

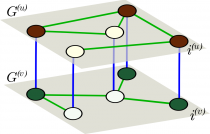
Pattern formation in multiplex networks

We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates

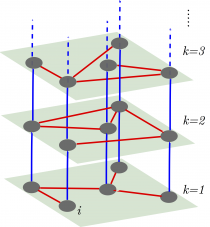
Multiplex networks: spectral properties

One of the more challenging tasks in the understanding of dynamical properties of models on top of complex networks is to capture the precise role of multiplex topologies. In a recent paper, Gómez et al. [Phys. Rev. Lett. 110, 028701

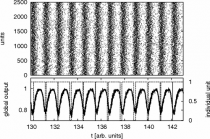
Two-state exitable systems

A two-state unit is considered as an abstract modification for an excitable system. Each state is characterized by a different waiting time distribution. This non-Markovian approach allows for a renewal process description of the system dynamics. Exact formulas for the