Bistable systems
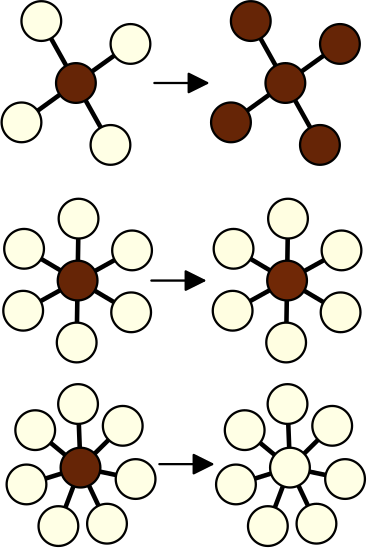
Stationary patterns in star networks of bistable units: Theory and application to chemical reactions
We present theoretical and experimental studies on pattern formation with bistable dynamical units coupled in a star network configuration. By applying a localized perturbation to the central or the peripheral elements, we demonstrate the subsequent spreading, pinning, or retraction of

Stationary patterns in star networks of bistable units: Theory and application to chemical reactions
We present theoretical and experimental studies on pattern formation with bistable dynamical units coupled in a star network configuration. By applying a localized perturbation to the central or the peripheral elements, we demonstrate the subsequent spreading, pinning, or retraction of
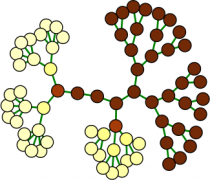
Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions
Experiments with networks of discrete reactive bistable electrochemical elements organized in regular and nonregular tree networks are presented to confirm an alternative to the Turing mechanism for the formation of self-organized stationary patterns. The results show that the pattern formation

Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions
Experiments with networks of discrete reactive bistable electrochemical elements organized in regular and nonregular tree networks are presented to confirm an alternative to the Turing mechanism for the formation of self-organized stationary patterns. The results show that the pattern formation
Tutorial 5 for WWCS2016
IPython Notebooks for the Tutorial 5 of the Winter Workshop on Complex Systems 2016 This python notebook solves a bistable system on a complex network and visualizes the solution Import networkx library import networkx as nx For the numerical integration
Tutorial 5 for WWCS2016
IPython Notebooks for the Tutorial 5 of the Winter Workshop on Complex Systems 2016 This python notebook solves a bistable system on a complex network and visualizes the solution Import networkx library import networkx as nx For the numerical integration
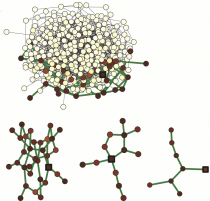
Feedback induced patterns in bistable networks
Effects of feedbacks on self-organization phenomena in networks of diffusively coupled bistable elements are investigated. For regular trees, an approximate analytical theory for localized stationary patterns under application of global feedbacks is constructed. Using it, properties of such patterns in

Feedback induced patterns in bistable networks
Effects of feedbacks on self-organization phenomena in networks of diffusively coupled bistable elements are investigated. For regular trees, an approximate analytical theory for localized stationary patterns under application of global feedbacks is constructed. Using it, properties of such patterns in
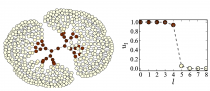
Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable

Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable