Posts Tagged 'Reaction-diffusion'
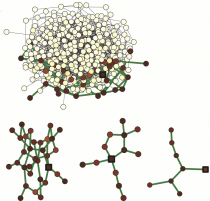
Feedback induced patterns in bistable networks
Effects of feedbacks on self-organization phenomena in networks of diffusively coupled bistable elements are investigated. For regular trees, an approximate analytical theory for localized stationary patterns under application of global feedbacks is constructed. Using it, properties of such patterns in

Feedback induced patterns in bistable networks
Effects of feedbacks on self-organization phenomena in networks of diffusively coupled bistable elements are investigated. For regular trees, an approximate analytical theory for localized stationary patterns under application of global feedbacks is constructed. Using it, properties of such patterns in
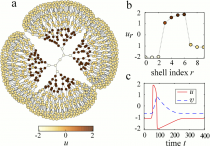
Excitable networks
Excitation waves are studied on trees and random networks of coupled active elements. Undamped propagation of such waves is observed in those networks. It represents an excursion from the resting state and a relaxation back to it for each node.

Excitable networks
Excitation waves are studied on trees and random networks of coupled active elements. Undamped propagation of such waves is observed in those networks. It represents an excursion from the resting state and a relaxation back to it for each node.
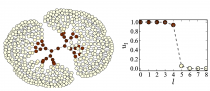
Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable

Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable
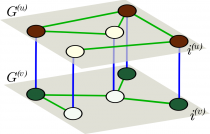
Pattern formation in multiplex networks
We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates

Pattern formation in multiplex networks
We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates