stationary patterns
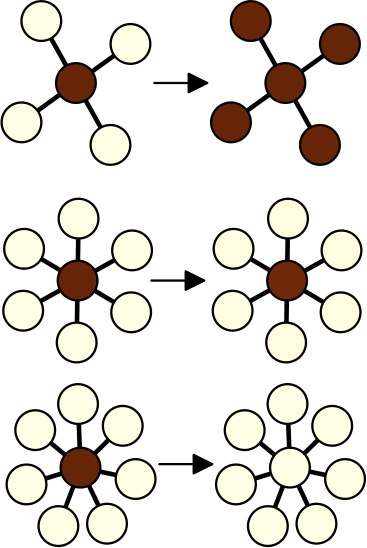
Stationary patterns in star networks of bistable units: Theory and application to chemical reactions
We present theoretical and experimental studies on pattern formation with bistable dynamical units coupled in a star network configuration. By applying a localized perturbation to the central or the peripheral elements, we demonstrate the subsequent spreading, pinning, or retraction of

Stationary patterns in star networks of bistable units: Theory and application to chemical reactions
We present theoretical and experimental studies on pattern formation with bistable dynamical units coupled in a star network configuration. By applying a localized perturbation to the central or the peripheral elements, we demonstrate the subsequent spreading, pinning, or retraction of
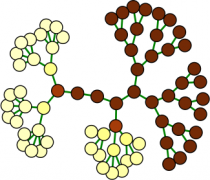
Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions
Experiments with networks of discrete reactive bistable electrochemical elements organized in regular and nonregular tree networks are presented to confirm an alternative to the Turing mechanism for the formation of self-organized stationary patterns. The results show that the pattern formation

Self-Organized Stationary Patterns in Networks of Bistable Chemical Reactions
Experiments with networks of discrete reactive bistable electrochemical elements organized in regular and nonregular tree networks are presented to confirm an alternative to the Turing mechanism for the formation of self-organized stationary patterns. The results show that the pattern formation
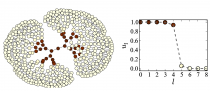
Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable

Bistable tree networks: Traveling and pinned fronts
Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable
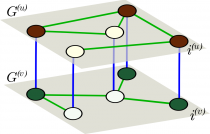
Pattern formation in multiplex networks
We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates

Pattern formation in multiplex networks
We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates