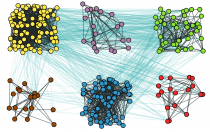
Chimera-like states in modular networks

Inspired by the ancient Greek mythological creature Chimera (χίμαιρα) which had a lion’s head, a goat’s body and a serpent’s tail, Abrams and Strogatz [1] coined the term “chimera states” for the counterintuitive self-organized phenomenon in which synchronous and desynchronous

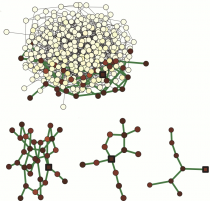
Feedback induced patterns in bistable networks

Effects of feedbacks on self-organization phenomena in networks of diffusively coupled bistable elements are investigated. For regular trees, an approximate analytical theory for localized stationary patterns under application of global feedbacks is constructed. Using it, properties of such patterns in

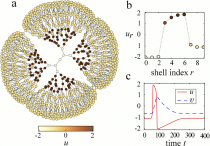
Excitable networks

Excitation waves are studied on trees and random networks of coupled active elements. Undamped propagation of such waves is observed in those networks. It represents an excursion from the resting state and a relaxation back to it for each node.

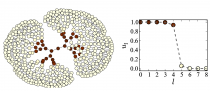
Bistable tree networks: Traveling and pinned fronts

Traveling fronts and stationary localized patterns in bistable reaction-diffusion systems have been broadly studied for classical continuous media and regular lattices. Analogs of such non-equilibrium patterns are also possible in networks. Here, we consider traveling and stationary patterns in bistable

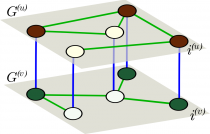
Pattern formation in multiplex networks

We study pattern formation in the new framework of multiplex networks, where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates

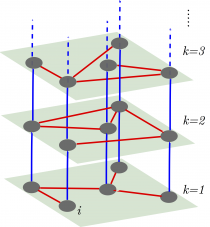
Multiplex networks: spectral properties

One of the more challenging tasks in the understanding of dynamical properties of models on top of complex networks is to capture the precise role of multiplex topologies. In a recent paper, Gómez et al. [Phys. Rev. Lett. 110, 028701